Fractions are a fundamental part of mathematics that allow us to express and compare quantities that are not whole numbers. They are used to represent ratios, proportions, and part-to-whole relationships, which are all important concepts in everyday life.
What is a fraction?
Fractions are fundamental ways to represent parts of wholes.Fractions are composed of two essential components: the numerator and the denominator.
Denominator: The bottom part of the fraction, indicating how many equal parts make up the whole.
Numerator: This is the top part of the fraction, representing how many parts of the whole you have.
Example 1 : Let’s grasp the concept of fractions with the following illustration: Imagine a set of 6 numbered boxes, out of which 2 boxes are filled with green colour.

Now, let’s determine the fraction representing the boxes filled with green colour:
Since a fraction signifies a part of a whole, we can calculate it by dividing the number of boxes filled with green colour by the total number of boxes.
Fraction of boxes filled with green colour = Number of Boxes filled with green colour / Total Number of Boxes
= 2/6
Similarly
Fraction of boxes without filled colour = Number of Boxes without filled colour / Total Number of Boxes
=. 4/6
Example 2 : Imagine a pizza cut into 4 equal parts, and one part has been eaten. This means there are 3 parts of the pizza remaining.
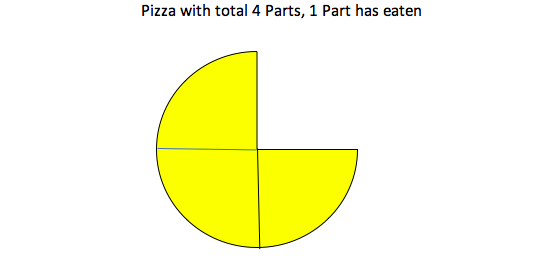
So, if we want to express the fraction of the remaining part, it will be:
Fraction of the remaining part of the pizza = 3/4
Similarly, the fraction of the eaten part would be:
Fraction of the eaten part = 1/4
Question & Solutions
Question: Mary has a pizza divided into 8 equal slices. She has eaten 3 of those slices. What fraction of the pizza has Mary eaten, and how many slices are left?
Solution :
let’s solve the question:
Mary has a pizza divided into 8 equal slices, and she has eaten 3 of those slices.
Fraction of pizza eaten by Mary: To find this, we can use the following formula:
Fraction eaten = (Number of slices eaten) / (Total number of slices)
In this case, Mary has eaten 3 slices out of a total of 8 slices:
Fraction eaten = 3 / 8
So, Mary has eaten 3/8 of the pizza.
Number of slices left: To find this, we subtract the slices Mary ate from the total number of slices:
Number of slices left = Total number of slices – Number of slices eaten
Number of slices left = 8 – 3 = 5 slices
So, Mary has 5 slices of pizza left.
Types of Fractions :
Fractions are more than just numbers; they come in various forms, each with its unique characteristics. In this exploration of fractions, let’s delve into the different types:
1. Proper Fractions:
Definition: Proper fractions are those where the numerator (the top number) is smaller than the denominator (the bottom number).
Example: Consider 1/2, 3/5, and 7/9; all are proper fractions.
2. Improper Fractions:
Definition: In improper fractions, the numerator is greater than or equal to the denominator.
Example: Think of 4/3, 5/4, and 9/9 as examples of improper fractions.
3. Mixed Numbers:
Definition: Mixed numbers combine whole numbers with fractions.
Example: 2 1/2 is a mixed number, which equals 2 + 1/2.
4. Equivalent Fractions:
Definition: Fractions are equivalent if they represent the same portion of a whole.
Example: Both 1/2 and 2/4 are equivalent fractions as they both signify half.
5. Like Fractions:
Definition: Like fractions have identical denominators.
Example: 1/4, 2/4, and 3/4 are like fractions, all sharing a denominator of 4.
6. Unlike Fractions:
Definition: Unlike fractions have different denominators.
Example: 1/4 and 1/3 are unlike fractions due to their differing denominators.
7. Unit Fractions:
Definition: Unit fractions have 1 as their numerator.
Example: 1/2, 1/3, and 1/10 are unit fractions, each representing one part of a whole.
8. Complex Fractions:
Definition: Complex fractions feature numerators and denominators that are fractions themselves.
Example: An example is (1/2)/(1/3), a complex fraction within fractions.
Understanding these types of fractions is vital for tackling various mathematical problems. Whether you’re baking, budgeting, or dealing with intricate calculations, fractions play a significant role in making sense of real-world scenarios. Embrace the diversity of fractions; they are the building blocks of mathematical versatility.
Exercise on Equivalent Fraction
How to Find Equivalent Fractions
To find equivalent fractions, you need to multiply or divide both the numerator and the denominator by the same nonzero number. Here are some example :-
Example 1. Find the 3 equivalent fraction of 3/4?
Solution :
3/4 X 2/2 = 6/8
3/4 X 3/3 = 9/12
3/4 X 4/4 = 12/16
Example 2. Find the 3 equivalent fraction on 4/5 ?
Solution :
4/5 X 5/5 = 20/25
4/5 X 6/6 = 24/30
4/5 X 8/8 = 32/ 40
Example3: Find an equivalent fraction to 2/5 with a denominator of 15.
Explanation: To find an equivalent fraction with a denominator of 15 for the fraction 2/5,
you need to determine what you can multiply the denominator (5) by to get 15.
In this case, you can multiply both the numerator (2) and the denominator (5) by 3:
(2/5) X (3/3) = 6/15
So, the equivalent fraction to 2/5 with a denominator of 15 is 6/15.
Example 4 : You have the fraction 3/4, and we want to find an equivalent fraction with a denominator of 12.
Solution:
- Start with the original fraction: 3/4.
- To get a denominator of 12, think about what you can multiply 4 by to make it 12. In this case, you need to multiply it by 3 because 4 X 3 = 12.
- Now, to keep the fraction equivalent, you should also multiply the numerator (3) by the same number you multiplied the denominator by, which is 3.
- Multiply the numerator and denominator:Numerator: 3 X 3 = 9 Denominator: 4 X3 = 12
3/4 X 3/3 = 9/12
So, the equivalent fraction to 3/4 with a denominator of 12 is 9/12.
You successfully found an equivalent fraction: 3/4 is the same as 9/12 when the denominator is 12
Conversion of Unlike fraction to like fraction
Unlike Fractions
Unlike fractions are fractions that have different denominators. For example, 1/2 and 3/4 are unlike fractions.
Like Fractions
Like fractions are fractions that have the same denominator. For example, 1/2 and 2/2 are like fractions.
Converting Unlike Fractions to Like Fractions
Converting Unlike Fractions to Like Fractions: To add or subtract fractions with different denominators, we need to make them like fractions, which means having the same denominator.
Here’s how you can do it:
Step 1: Find a Common Denominator
- Determine the least common multiple (LCM) of the denominators of the given unlike fractions. The LCM is the smallest multiple that both denominators share.
Step 2: Create Equivalent Fractions
- For each fraction, create an equivalent fraction with the common denominator found in Step 1. To do this, you’ll multiply both the numerator and denominator of each fraction by the same value.
Step 3: Perform the Operation
- Once you have like fractions, you can easily perform addition or subtraction as needed.
Let’s illustrate this process with an example:
Example: Converting Unlike Fractions to Like Fractions
- We want to convert unlike fraction 1/3 and 2/5 to like fraction . First, find the common denominator.
- The LCM of 3 and 5 is 15.
- Now, create equivalent fractions for both fractions with a denominator of 15.
- For 1/3: Multiply both the numerator and denominator by 5. You get (1X5)/(3 X5) = 5/15.
- For 2/5: Multiply both the numerator and denominator by 3. You get (2X3)/(5 X3) = 6/15.
- Now, both fractions have the same denominator, and you can add them: 5/15 + 6/15 = 11/15
