The Basics of Prime Factorization: Common Factor, Highest Common Factor

Prime Factorization:

We know that a number can be expressed as the product of its factors. These factors can be composite or prime numbers. A prime factorization occurs when the product of all the factors is only prime numbers.

Prime Factorization Method

The process of breaking down a number into its prime numbers is called the prime factorization Method.

There are Two types of prime factorization methods:

1. Factor Tree Method
2. Long Division Method

Prime Factorization through The Factor Tree Method :

A factor tree is a graphical representation used in mathematics to break down a composite number into its prime factors. Prime factors are the prime numbers that, when multiplied together, give you the original composite number.

Here’s how you construct a factor tree:

1. Start with the composite number you want to factorize. This number is usually at the top of the tree.
2. Find two factors of the composite number that, when multiplied together, equal the original number. These factors can be prime or composite.
3. Write these two factors as branches stemming from the top number.
4. Continue this process for each branch until you reach a point where all the branches end in prime numbers. These prime numbers are the prime factors of the original composite number.
5. Write down the prime factors along with their multiplicities (how many times they appear as factors).

Factor trees are useful for finding the prime factorization of a number, which can be important in various areas of mathematics, including number theory and algebra. They also help you understand the building blocks of a number and can be used for simplifying fractions and solving certain types of mathematical problems.

Example for the Factor Tree Method:

Let’s explain through example of the number 48

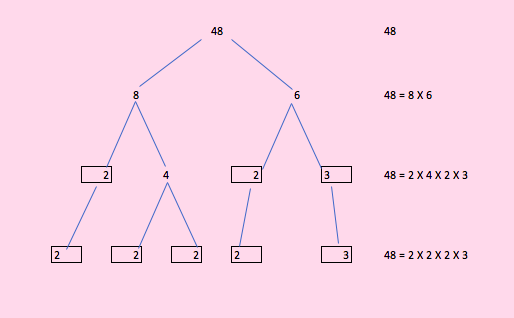
Prime Factorization through The Long Division Method:

Prime factorization through the long division method is a systematic way to find the prime factors of a number by repeatedly dividing it by prime numbers. Here’s how you can do it:

Let’s use the number 72 as an example to find its prime factorization using the long division method:

Common Factor

A common factor is a number that divides two or more numbers exactly.In other words, it’s a number that is a factor of more than one integer.

For example, let’s consider the numbers 12 and 18.

Factor of 12 = ( 1, 2, 3, 4, 6, 12)

Factor of 18 = (1, 2, 3, 6, 9, 18 )

In this case, the common factors of 12 and 18 are 1, 2, 3, and 6 because these numbers can divide both 12 and 18 without leaving a remainder.

Highest Common Factor ( HCF)

The highest common factor (HCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides evenly into two or more numbers. In other words, it’s the greatest number that is a common factor in a set of numbers.

For example, let’s consider the numbers 12 and 18. The common factors of 12 and 18 are 1, 2, 3, and 6 (we already explained it above). Among these common factors, the largest one is 6. Therefore, the highest common factor (HCF) or greatest common divisor (GCD) of 12 and 18 is 6.

Finding the HCF or GCD is important in mathematics for various purposes, such as simplifying fractions, reducing ratios to their simplest form, and solving problems involving factors or divisibility. It’s a fundamental concept in number theory and plays a significant role in many mathematical calculations.